二項分布・ポアソン分布・正規分布
最初に、二項分布の総和・平均値・分散を求める。
次に、二項分布から、ポアソン分布を導出する。
続いて、ポアソン分布の総和・平均値・分散及び、3次のモーメントを求める。
最後に、二項分布から正規分布を導出する。
特に、二項分布から正規分布を導出する手順が載っているテキストは少ない。
二項分布(ベルヌーイ分布)
ある特定の事象が起こる確率をpとする。
また、余事象が起こる確率をq≡1-pとする。
pが一定のとき、試行は独立であり、ベルヌーイ試行である、という。
n回の試行のうち、x回起こる確率は、次の関数:

で与えられる。この分布を二項分布、または、ベルヌーイ分布の確率密度関数と呼ぶ。
まず最初に、二項分布の総和を求める。その総和は、二項定理より、

と計算され、確率の和が1であることを示す。
次に、二項分布の平均値を求める。ここで、求める平均値を

と置いて、総和の式:

の両辺をpで微分すると、
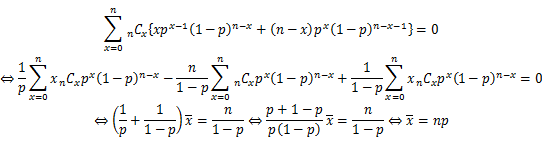
という計算結果を得る。
続いて、二項分布の分散を求める。まず、求める分散であるが、
分布の総和が1であることから、

と式変形できる。この式:

は、「分散は、『二乗の平均』から『平均の二乗』を引いたものに等しい。」
ことを意味している。
そこで、「二乗の平均」を求める為に、

の両辺をpで微分すると、

という計算結果が得られるので、分散は、平均値がnpであることを代入して、

と求められる。
ポアソン分布
二項分布において、ある特定の事象が起こる確率pが極めて低い場合を考える。
しかし、試行回数nが極めて大きければ、両者の積は一定に保たれる、とする。即ち、

と置いて、二項分布の極限を考えることになる。
二項分布にpをλで表した式を代入し、
n→∞の極限をとると、

と計算できる。ここで得られた、

という分布は、ポアソン分布の確率密度関数と呼ばれる。
まず最初に、ポアソン分布の総和を求める。
その総和は、指数関数のマクローリン展開より、

と計算され、やはり確率の和が1となることを示している。
次に、ポアソン分布の平均値を求める。ここで、求める平均値は、
やはり、指数関数のマクローリン展開を用いて、

という計算結果が得られる。
さて、ポアソン分布の分散を求めるわけだが、その前に、
「分散は、『二乗の平均』から『平均の二乗』を引いたものに等しい。」
ということを思い出そう。まず、「二乗の平均」を求める必要があるのである。
x=(x-1)+1と分解して、「二乗の平均」:

という計算結果が得られるので、
分散は、平均値がλであることを代入して、

と求められる。
最後に、ポアソン分布の3次のモーメント:m3を求めてみよう。
これは、分散の時と同様の手法が適用できて、

と式変形できる。今度は、分散の時ほど単純ではないが、「二乗の平均」の他に
「三乗の平均」も必要になってくることが分かるだろう。
そこで、まず、「三乗の平均」を計算すると、

となるから、これを用いて、3次のモーメント:m3は、

と求められる。4次以上の高次のモーメントも同様に計算できるが、
実際に逐一計算するのは煩雑なので、モーメント母関数を用いた方が便利である。
詳細は、「高次のモーメントとモーメント母関数」を参照。
正規分布(ガウス分布)
二項分布において、試行回数nが非常に大きい場合を考える。
nとxが非常に大きいとして、
二項分布の確率密度関数において、スターリングの公式:

を適用すると、

という形に式変形することが出来る。
ここで、xの平均値をμ≡npと置き、
平均からのズレ(揺らぎ)をξ≡x-μと置く。
また、余事象の確率をq≡1-pと置く。すると、

と式変形できるので、これらをf(x)に代入する。その際、

という3つのパーツに分解する。B及びCは、
後で行う近似の準備の為に、逆数のマイナス乗という形に変形する。
Aは、n>>1のとき、

と式変形できる。ところで、n>>1のとき、B及びCの自然対数をとると、
ln(1+x)及び、ln(1-x)という形にできるので、
「無限等比級数の和とテイラー展開」で導出した式より、

という近似を用いて、

と近似する。これらをf(x)の式に代入して、

を得る。ここで、ξの3次以上のオーダー:O(ξ3)は無視すると、

と計算できる。ここで得られた、

という分布は、正規分布、または、ガウス分布の確率密度関数と呼ばれる。
特に、平均値μ=0、分散σ2=12とした分布:

は、標準正規分布と呼ばれる。