マクローリン展開

グラフ作成ツール「gnuplot」を用いて、マクローリン展開(Maclaurin expansion)をグラフに描いてみた。
一般に、マクローリン展開は、

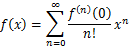
で表される。今回、近似の対象に用いた関数 y＝f(x)(赤)は
f(x)＝e^x，f(x)＝cos x，f(x)＝sin x， f(x)＝cosh x，f(x)＝sinh x
であるが、これに対し、いずれの関数のグラフも
第1項(緑) →第2項(青) →第3項(紫) →第4項(水色) →第5項(茶色)
の順に近似の精度が高くなっている事が理解できるだろう。
これらのグラフからは、マクローリン展開が水平方向への補正による、
「horizontal」な近似であるという印象を受ける。

目次

f(x)＝e^xのマクローリン展開

f(x)＝e^xのマクローリン展開は、次式で表される。

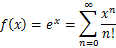
上記の結果をグラフ作成ツール「gnuplot」を用いて、グラフ化する。
「gnuplot」を起動して、以下のコマンドを入力し、グラフを生成する。
（勿論、出力先のディレクトリは、各自の環境に応じて適宜変更する。）

set terminal png set xrange[-5:5] set yrange[-5:5] set xtics 0.5 set ytics 0.5 set grid plot exp(x) replot 1 replot 1+x replot 1+x+x**2/2! replot 1+x+x**2/2!+x**3/3! set output 'c:\temp\maclaurinofexp.png' replot 1+x+x**2/2!+x**3/3!+x**4/4! exit

この方法により生成したグラフを以下に示す。


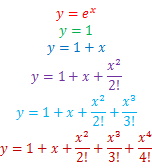
GIFアニメーション作成ソフトでGIFアニメーション化したグラフ：

f(x)＝cos xのマクローリン展開

f(x)＝cos xのマクローリン展開は、次式で表される。

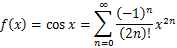
上記の結果をグラフ作成ツール「gnuplot」を用いて、グラフ化する。
「gnuplot」を起動して、以下のコマンドを入力し、グラフを生成する。
（勿論、出力先のディレクトリは、各自の環境に応じて適宜変更する。）

set terminal png set xrange[-5:5] set yrange[-5:5] set xtics 0.5 set ytics 0.5 set grid plot cos(x) replot 1 replot 1-x**2/2! replot 1-x**2/2!+x**4/4! replot 1-x**2/2!+x**4/4!-x**6/6! set output 'c:\temp\maclaurinofcos.png' replot 1-x**2/2!+x**4/4!-x**6/6!+x**8/8! exit

この方法により生成したグラフを以下に示す。
f(x)は偶数次の項のみで近似できることから、
cos xが偶関数であることが分かるだろう。


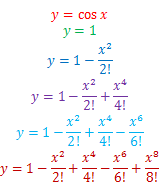
GIFアニメーション作成ソフトでGIFアニメーション化したグラフ：

f(x)＝sin xのマクローリン展開

f(x)＝sin xのマクローリン展開は、次式で表される。

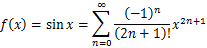
上記の結果をグラフ作成ツール「gnuplot」を用いて、グラフ化する。
「gnuplot」を起動して、以下のコマンドを入力し、グラフを生成する。
（勿論、出力先のディレクトリは、各自の環境に応じて適宜変更する。）

set terminal png set xrange[-5:5] set yrange[-5:5] set xtics 0.5 set ytics 0.5 set grid plot sin(x) replot x replot x-x**3/3! replot x-x**3/3!+x**5/5! replot x-x**3/3!+x**5/5!-x**7/7! set output 'c:\temp\maclaurinofsin.png' replot x-x**3/3!+x**5/5!-x**7/7!+x**9/9! exit

この方法により生成したグラフを以下に示す。
f(x)は奇数次の項のみで近似できることから、
sin xが奇関数であることが分かるだろう。


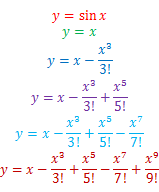
GIFアニメーション作成ソフトでGIFアニメーション化したグラフ：

オイラーの公式の導出とその応用

f(x)＝e^xのマクローリン展開の式において、 x＝iθを代入すると、

より、オイラーの公式：
e^iθ ＝cos θ＋isin θ
を得る。特に、θ＝πのとき、
e^iπ＝－1
となる。これは、複素数平面上での180度回転が、
「折り返し」であることを意味する。

ここで、オイラーの公式において、θの代わりに、－θとすると、
e^－iθ ＝cos θ－i sin θ
となるが、両式の辺々を加え合わせると、
e^iθ ＋e^－iθ＝2cos θ
cos θ＝(e^iθ ＋e^－iθ)/2
となって、余弦関数を複素指数関数の式で表すことができる。
同様に、両式の辺々の差分をとると、
e^iθ －e^－iθ＝2i sin θ
sin θ＝(e^iθ －e^－iθ)/2i
となって、正弦関数も複素指数関数の式で表すことができる。

さらに、オイラーの公式において、θ＝α ± βを代入すると、
cos (α ± β)＋i sin (α ± β) ＝e^{(α ± β)} ＝e^αe ^{± β}
＝(cos α cos β ∓ sin α sin β) ＋i (sin α cos β ± cos α sin β)
ここで、実部と虚部の独立性により、
cos (α ± β) ＝cos α cos β ∓ sin α sin β　（複号同順）
sin (α ± β) ＝sin α cos β ± cos α sin β　（複号同順）
となるから、余弦関数と正弦関数に関して、三角関数の加法定理を得る。

また、下の式を上の式で割り、分子分母をcos α cos βで割ると、

となり、正接関数に関しても、三角関数の加法定理を得る。

f(x)＝cosh xのマクローリン展開

f(x)＝cosh xのマクローリン展開は、次式で表される。

上記の結果をグラフ作成ツール「gnuplot」を用いて、グラフ化する。
「gnuplot」を起動して、以下のコマンドを入力し、グラフを生成する。
（勿論、出力先のディレクトリは、各自の環境に応じて適宜変更する。）

set terminal png set xrange[-10:10] set yrange[-10:210] set xtics 1 set ytics 10 set grid plot cosh(x) replot 1 replot 1+x**2/2! replot 1+x**2/2!+x**4/4! replot 1+x**2/2!+x**4/4!+x**6/6! set output 'c:\temp\maclaurinofcosh.png' replot 1+x**2/2!+x**4/4!+x**6/6!+x**8/8! exit

この方法により生成したグラフを以下に示す。
やはりf(x)は偶数次の項のみで近似できることから、
cosh xも偶関数であることが分かるだろう。

f(x)＝sinh xのマクローリン展開

f(x)＝sinh xのマクローリン展開は、次式で表される。

上記の結果をグラフ作成ツール「gnuplot」を用いて、グラフ化する。
「gnuplot」を起動して、以下のコマンドを入力し、グラフを生成する。
（勿論、出力先のディレクトリは、各自の環境に応じて適宜変更する。）

set terminal png set xrange[-10:10] set yrange[-500:500] set xtics 1 set ytics 50 set grid plot sinh(x) replot x replot x+x**3/3! replot x+x**3/3!+x**5/5! replot x+x**3/3!+x**5/5!+x**7/7! set output 'c:\temp\maclaurinofsinh.png' replot x+x**3/3!+x**5/5!+x**7/7!+x**9/9! exit

この方法により生成したグラフを以下に示す。
やはりf(x)は奇数次の項のみで近似できることから、
sinh xも奇関数であることが分かるだろう。

双曲線関数の加法定理

双曲線関数にも、双曲線関数版のオイラーの公式の様な式が存在するのだろうか。
実際に、実指数関数f(x)＝e^xのマクローリン展開の式において、

と計算すると、実指数関数e^xを偶関数部分と奇関数部分に分解することができて、
e^x＝cosh x＋sinh x
という、双曲線関数版のオイラーの公式の様な式は、一応導けるが、本来、
実指数関数e^xを偶関数部分と奇関数部分に分解し、前者を双曲線余弦関数cosh x、
後者を双曲線正弦関数sinh xと呼ぶように定義したのであるから、実指数関数が、
双曲線余弦関数と双曲線正弦関数の和で表せるというのは、自明の結果に過ぎない。

上記の理由により、三角関数の加法定理のときみたいに、実部と虚部の独立性を用いて、
双曲線関数の加法定理を導出することはできないが、先程のように、
複素指数関数の式で、余弦関数や正弦関数を表すことはできるため、
双曲線余弦関数cosh xや、双曲線正弦関数sinh xの定義の式と比較して、
双曲線余弦関数cosh xや、双曲線正弦関数sinh xの加法定理：
cosh (α ± β) ＝cosh α cosh β ± sinh α sinh β　（複号同順）
sinh (α ± β) ＝sinh α cosh β ± cosh α sinh β　（複号同順）
及び、双曲線正接関数tanh xの加法定理：

を導出することができる。

Shadow Academy トップへ戻る