楕円積分と楕円関数

単振り子の周期に関して、第1種楕円積分が現れ、
楕円の弧長に関して、第2種楕円積分が現れる。
また、第1種楕円積分の逆関数として、楕円関数が定義される。
楕円積分と完全楕円積分、ルジャンドル標準形とヤコビ標準形等、
複数の形式が存在して混乱を招く可能性があるので、
これらを整理してみることにした。

第1種楕円積分

単振り子の微分方程式：

の両辺に

dθ

を掛けると、

となる。これを積分して、

とする。ここで、振り子がθ＝θ_mで静止したとすると、

を得る。従って、得られた積分定数Cを代入して、

となる。対称性から、0≤θ≤πのみを考えればよいので、

の様に、変数を分離することが出来る。ここで積分範囲を
とすると、積分して

を得る。ここで、t_mは、周期の4分の1である。

ここで、

と置く。この変数変換の式の両辺を微分すると、

となり、また、この変数変換の式の両辺を二乗すると、

であるので、両式より、

となって、積分変数をθからφへと変換することが出来た。
積分範囲は、θ＝θ_m（0≤θ≤π）のとき、
sinφ＝1⇔φ＝π/2なので、0≤φ≤π/2である。

再び、t_mの式に戻って、半角の公式を適用し、
積分変数をθからφへと変換すると、

を得る。ここで、

と置くと、t_mは、ルジャンドル（Legendre）標準形の第1種完全楕円積分：

を用いて、

と表せる。K(k)は、ルジャンドル標準形の第1種楕円積分：

において、φ＝π/2とした場合である。

ルジャンドル標準形の第1種完全楕円積分において、x≡sinφと置くと、

と積分変数を変換することが出来て、φ＝π/2のとき、x＝1であるから、

と書ける。これをヤコビ（Jacobi）標準形の第1種完全楕円積分と呼ぶ。
これは、ヤコビ標準形の第1種楕円積分：

において、x＝1とした場合である。

楕円関数

ヤコビ標準形の第1種楕円積分を

と置き、その逆関数として、sn（エスエヌ）関数：
x＝sn y＝sn(y, k)
を定義する。k＝0のとき、

及び、k＝1のとき、

となって、正弦関数や双曲線正接関数になることが分かる。

また、ルジャンドル標準形の第1種楕円積分において、

と置くと、その逆関数として、振幅関数：
φ＝am y＝am(y, k)
が定義される。ここで、
sn y＝x＝sin φ＝sin (am y)
であるが、さらにこれに対して、cn（シーエヌ）関数：

及び、dn（ディーエヌ）関数：

を定義する。この定義により、k＝0のとき、

となって、それぞれ余弦関数と1になることが分かり、また、k＝1のとき、

となって、双方共に双曲線余接関数になることが分かる。

楕円関数を微分してその導関数を求めよう。sn関数の定義により、

が得られるので、このsn関数の導関数を用いて、cn関数の導関数：

及び、dn関数の導関数：

が得られる。

第2種楕円積分

楕円の長径をa、短径をbとし、長径方向にx軸、短径方向にy軸をとり、
動径とx軸とのなす角をφと置いて、角度φに対する楕円の弧長を考える。
楕円の方程式：

x²		y²
	＋		＝1
a²		b²

において、x座標及び、y座標を媒介変数φで表すと、
x＝acos φ
y＝bsin φ
となるので、微小要素の変数変換は、
dx＝－asin dφ
dy＝bcos dφ
より、楕円の弧長は、微小要素：

を積分した式：

により得られる。ここで、

をルジャンドル標準形の第2種楕円積分と呼び、
特に、φ＝π/2とした場合：

をルジャンドル標準形の第2種完全楕円積分と呼ぶ。

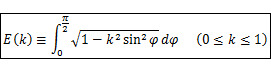
第1種楕円積分の時と同様、x≡sinφと置くと、ヤコビ標準形の第2種楕円積分：

を得る。特に、x＝1とした場合：

をヤコビ標準形の第2種完全楕円積分と呼ぶ。

ところで、
sin φ ＝ sn y
の両辺を微分すると、
cos φ dφ ＝ cn y dn y dy
となるが、ここで、
cos φ ＝ cn y
であったから、両辺を割ってやると、
dφ ＝ dn y dy
となる。これらを用いて、第2種楕円積分は、

と変形でき、第2種楕円積分が、dn² y の積分で与えられることが分かる。

また、第2種完全楕円積分E(k)を母数kで微分すると、

となり、第1種完全楕円積分K(k)と第2種完全楕円積分E(k)に関する一次式で表される。

楕円関数の加法定理

まず、f(u)≡sn u、f(v)≡sn vと定義すると、
k＝0のとき、f(u)＝sin u、f(v)＝sin vとなり、
k＝1のとき、f(u)＝tanh u、f(v)＝tanh vとなる。
従って、sn関数の加法定理は、k＝0のとき、正弦関数sin (u±v)の加法定理と一致し、
k＝1のとき、双曲線正接関数tanh (u±v)の加法定理と一致しなければならない。
正弦関数の加法定理と双曲線正接関数の加法定理を以下に示す。

ここで、正弦関数sin (u±v)の加法定理を少し変形してあるが、
余弦関数cosは、正弦関数sinの導関数として、表すことが出来る。
同様に、双曲線正接関数tanhの導関数は、
双曲線正割関数sechの二乗で表すことも出来るので、
これと同様の形式で書くと、双曲線正接関数tanh (u＋v)の加法定理は、
次のように変形することが出来る。

両者を比較し、母数kが、0と1の時の条件を満たすような式として、

という形を仮定する(この様な操作を「内挿」と呼ぶ)。
これは確かに、題意の条件を満たすので、
sn関数の導関数を代入して、sn関数の加法定理：

を得る。或いは、分子分母に sn u cn v dn v－sn v cn u dn u を掛けて、

と書くこともできる。